Trees-Mazes-Python
Now that we have maze generation working, it’s time to get started on solving our maze.
We’ll solve our generated maze with two different methods:
- Randomized, pre-order depth first search (similar to how we generated the maze)
- Breadth first search
Using depth first search will generally be quicker but implementing both DFS and BFS will help you visualize each search algorithm.
More Bit Manipulation!
Go back to maze.py so we can finish up a few more methods needed for DFS solving of a maze.
cell_neighbors
First off, let’s update cell_neighbors. cell_neighbors is supposed to use state to determine which neighbors are important – we only implemented it for state == 'create'. When state == 'solve', we only want neighbors that are accessible (no wall in their direction) and unvisited (are not on a backtrack path or solution path yet). We’ll have to use both bitwise OR and bitwise AND for this.
[action]
Complete the implementation of
cell_neighborsso that it:creates empty list of neighbors for each direction calculate new cell from cell if new cell in that direction is within the bounds of maze if state is create and all of new cell's walls are up add (new cell index, COMPASS index of direction) to neighbors if state is solve and no wall between cell and new cell if new cell not on solution or backtrack path add (new cell index, COMPASS index of direction) to neighbors return neighbors
[solution]
The completed
cell_neighborsmethod should look like this:def cell_neighbors(self, cell): x, y = self.x_y(cell) neighbors = [] for i in range(4): new_x = x + COMPASS[i][0] new_y = y + COMPASS[i][1] if self.cell_in_bounds(new_x, new_y): new_cell = self.cell_index(new_x, new_y) if self.state == 'create': if not (self.maze_array[new_cell] & WALL_BITS): neighbors.append((new_cell, i)) elif self.state == 'solve': if (self.maze_array[cell] & WALLS[i]): if not (self.maze_array[new_cell] & (BACKTRACK_BITS | SOLUTION_BITS)): neighbors.append((new_cell, i)) return neighbors
self.maze_array[cell] & WALL_BITSwill be zero ifcellhas a wall in the direction ofnew_cell.(BACKTRACK_BITS | SOLUTION_BITS)combines the two bit masks. That means that you can use(self.maze_array[new_cell] & (BACKTRACK_BITS | SOLUTION_BITS))to check if the cell contains any solution or backtrack path data.
visit_cell
visit_cell needs to wipe out all the solution bits of from_cell and set them to the current direction. Then it needs to add backtrack bits to to_cell pointing in the direction of from_cell.
We’ll need two new bitwise operators to do this:
- The compliment operator (
~in Python) – this flips all the bits. Zeros become ones and ones become zeros.~0b1010evaluates to0b0101. We’ll use this to invertSOLUTION_BITS. - The left bit shift operator (
<<in Python) – this moves all the bits over.0b1111 << 8evaluates to0b111100000000. We’ll use this to shift values fromWALLSandOPPOSITE_WALLSto the right position for updating solution bits and backtrack bits respectively.
Take some time to play around with ~ and << in the Python interpreter.
[action]
Complete the implementation of
visit_cell. It should clear the solution bits out offrom_cell, update solution bits infrom_cellusingWALLS[compass_index], update the backtrack bits into_cellusingOPPOSITE_WALLS[compass_index]. Leave the call todraw_connect_cellsor else the maze visualization will not be updated!
[solution]
The completed
visit_cellmethod should look like this:def visit_cell(self, from_cell, to_cell, compass_index): self.maze_array[from_cell] &= ~SOLUTION_BITS self.maze_array[from_cell] |= (WALLS[compass_index] << 8) self.maze_array[to_cell] |= (OPPOSITE_WALLS[compass_index] << 12) self.draw_visited_cell(from_cell)
backtrack
backtrack is a simple one. All we have to do is clear out the solution bits of cell.
[action]
Complete the implementation of
backtrack.
[solution]
The completed
backtrackmethod should look like this:def backtrack(self, cell): self.maze_array[cell] &= ~SOLUTION_BITS self.draw_backtracked_cell(cell)
Solving with Depth First Search
The pseudocode below should look very familiar. There is not much of a difference between maze generation and maze solving using DFS.
Pseudocode for Solving a Maze with DFS
create a stack for backtracking
set current cell to 0
set visited cells to 0
while current cell not goal
get unvisited neighbors using cell_neighbors
if at least one neighbor
choose random neighbor to be new cell
visit new cell using visit_cell
push current cell to stack
set current cell to new cell
add 1 to visited cells
else
backtrack current cell using backtrack method
pop from stack to current cell
call refresh_maze_view to update visualization
set state to 'idle'
[action]
Implement the pseudocode above in the
solve_dfsfunction ofsolve_maze.py. Runpython3 solve_maze.py dfsto see if your maze is getting solved correctly!
If you did everything right, your DFS solver should look like this:
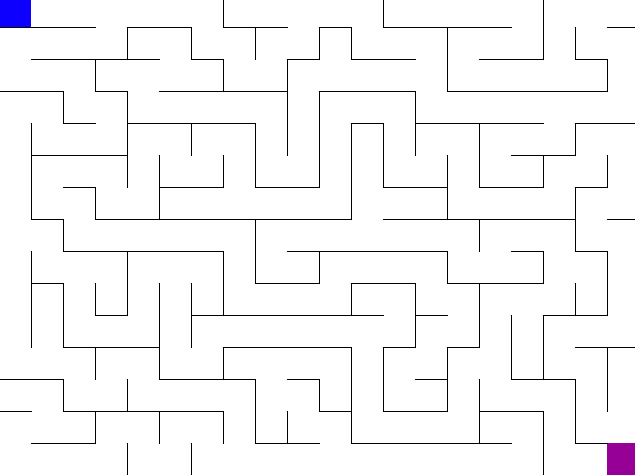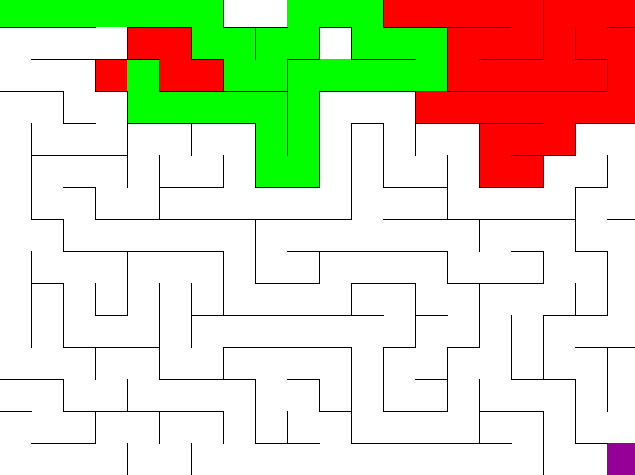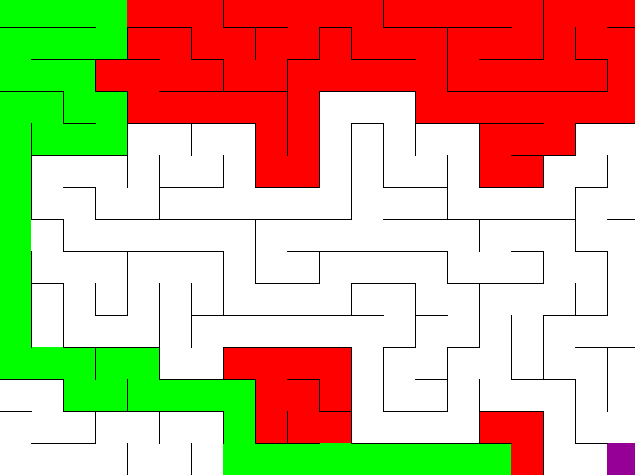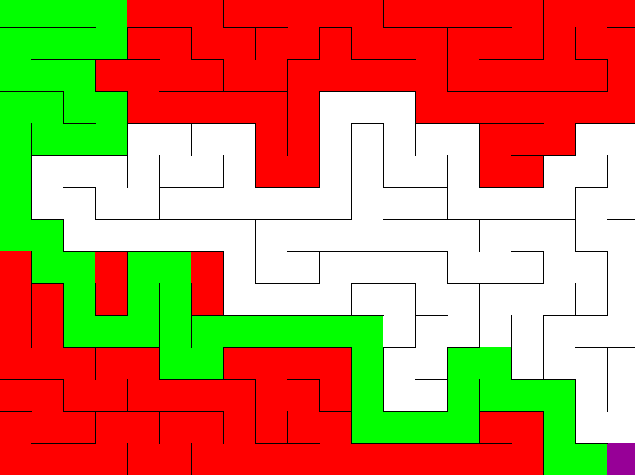
Bit Manipulation for BFS
bfs_visit_cell
bfs_visit_cell is more simple than visit_cell used in DFS. It only needs to set the backtrack bits for cell to point towards the cell it came from.
[action]
Complete the implementation of
bfs_visit_cell.
[solution]
The completed
bfs_visit_cellmethod should look like this:def bfs_visit_cell(self, cell, from_compass_index): self.maze_array[cell] |= (OPPOSITE_WALLS[from_compass_index] << 12) self.draw_bfs_visited_cell(from_cell)
reconstruct_solution
reconstruct_solution constructs a path from the start cell (root node) to cell by following the backtrack bits to build it in reverse. It should set the solution bits along the way.
[action]
Complete the implementation of
reconstruct_solutionusing the following pseudocode:draw cell as part of solution path with draw_visited_cell isolate the four backtrack bits to previous cell bits set i to index of previous cell bits in WALLS use i to calculate index of previous cell, set to previous cell update solution bits of previous cell to point towards cell call refresh_maze_view to update visualization if previous cell not start cell, reconstruct_solution(previous cell)
[solution]
The completed
reconstruct_solutionmethod should look something like this:def reconstruct_solution(self, cell): self.draw_visited_cell(cell) prev_cell_bits = (self.maze_array[cell] & BACKTRACK_BITS) >> 12 try: i = WALLS.index(prev_cell_bits) except ValueError: print('ERROR - BACKTRACK BITS INVALID!') x, y = self.x_y(cell) prev_x = x + COMPASS[i][0] prev_y = y + COMPASS[i][1] prev_cell = self.cell_index(prev_x, prev_y) self.maze_array[prev_cell] |= (OPPOSITE_WALLS[i] << 8) self.refresh_maze_view() if prev_cell != 0: self.reconstruct_solution(prev_cell)
Solving with Breadth First Search
Breadth first search visits all immediate children in order. We’ll be using the pseudocode below to implement BFS to solve some mazes.
Pseudocode for Solving a Maze with BFS
create a queue
set current cell to 0
set in direction to 0b0000
set visited cells to 0
enqueue (current cell, in direction)
while current cell not goal and queue not empty
dequeue to current cell, in direction
visit current cell with bfs_visit_cell
add 1 to visited cells
call refresh_maze_view to update visualization
get unvisited neighbors of current cell using cell_neighbors, add to queue
trace solution path and update cells with solution data using reconstruct_solution
set state to 'idle'
[action]
Implement the pseudocode above in the
solve_bfsfunction ofsolve_maze.py. Runpython3 solve_maze.py bfsto see if your maze is getting solved correctly!
If you did everything right, your BFS solver should look like this:
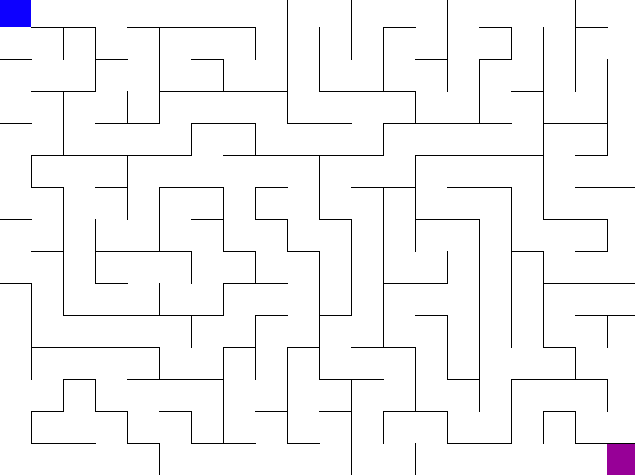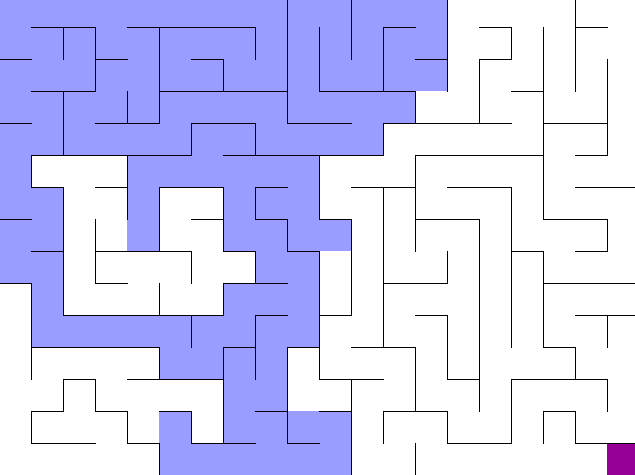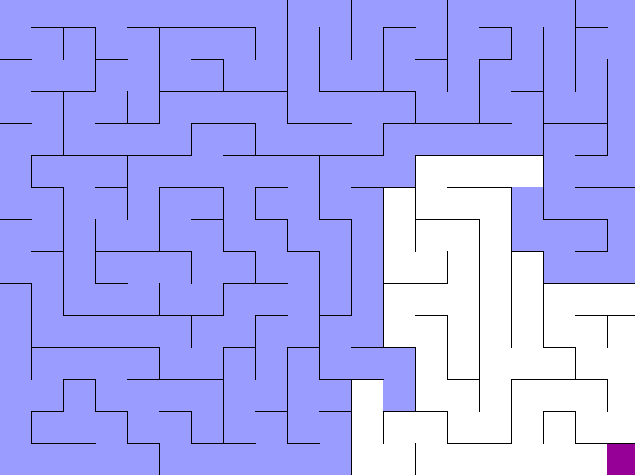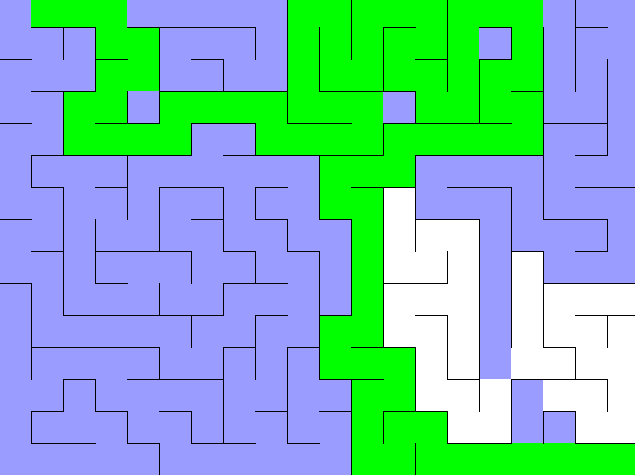
Stretch Goals
If you’re enjoying this and want to do more, here are some ideas:
- Complete
solution_arraymethod to return an array of cardinal directions (N, S, E, W) to get from start cell to goal cell - Implement A* search, A* uses “heuristics” to intelligently decide which neighbor to explore next
- Write methods to save mazes to file and load mazes from file, take advantage of the 16-bit cell data structure!